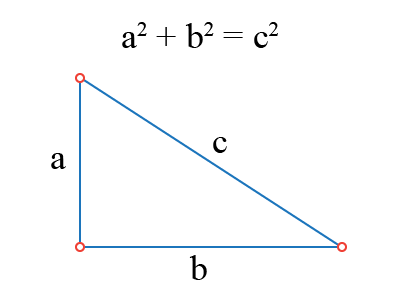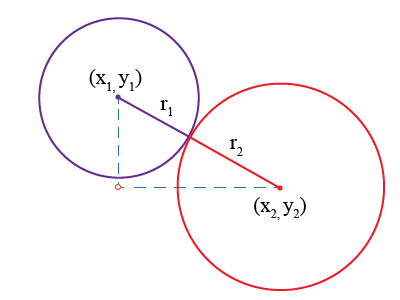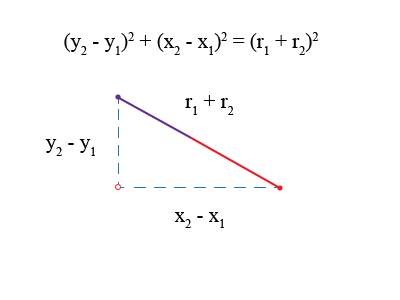[SOLVED] Modifying nearestToEntity() to nearestCircleToCircle

(Bora Kasap) #1

thats the function that flashpunk have in the world class

public function nearestToEntity(type:String, e:Entity, useHitboxes:Boolean = false):Entity
		{
			if (useHitboxes) return nearestToRect(type, e.x - e.originX, e.y - e.originY, e.width, e.height);
			var n:Entity = _typeFirst[type],
				nearDist:Number = Number.MAX_VALUE,
				near:Entity, dist:Number,
				x:Number = e.x - e.originX,
				y:Number = e.y - e.originY;
			while (n)
			{
				if (n != e)
				{
					dist = (x - n.x) * (x - n.x) + (y - n.y) * (y - n.y);
					if (dist < nearDist)
					{
						nearDist = dist;
						near = n;
					}
				}
				n = n._typeNext;
			}
			return near;
		}

But i need a function something like that for my game because i use radial collisions based on distances in my game, i have “public var radius:Number” variable in my entities.

 nearestCircleToCircle(type:String, e:Entity, useRadius:Boolean = false):Entity

can anybody help me about that?

(Bora Kasap) #2

i just changed the dist formula

x:Number = e.x - e.originX,
y:Number = e.y - e.originY;
radius:Number = e.radius;

dist = Math.sqrt((x − n.x)*(x − n.x) + (y − n.y)*(y − n.y)) − (radius + n.radius);

but now, i get an error about syntax for each “n” in my formula :S

“Syntax error: expecting rightparen before n.”

(Bora Kasap) #3

oh done… sorry for disturbing

(MartĂ­ Angelats i Ribera) #4

Just a side note: I recommend recommend not to use the Math.sqrt function if it’s possible becouse is a slow function.

(Bora Kasap) #5

i don’t know is it possible or not, what do you suggest instead of it for my situation? :confused:

(Jacob Albano) #6

Since you don’t need the actual distance (just the lowest distance), use the squared distance.Just remove Math.sqrt.

(Bora Kasap) #7

ok i tried, but it doesn’t work with different sized circles.

(Kyle) #8

It just means that you disregard getting the square roots. Just compare the ‘square’ of the distances. So in your case for example, it’s like:

// The distance will be the square of the actual distance now(NO Math.sqrt)
distSqrd = (x − n.x)*(x − n.x) + (y − n.y)*(y − n.y) − (radius + n.radius);
...
...
// Then in the if statement
// Compare the 'squares' of the distances
if (distSqrd < nearDistSqrd)
{
    // Blah blah blah
}

The result will just be the same regardless. It’s just that it will be easier for the computer to compute.

(Bora Kasap) #9

but i really tried, and it is really doesn’t work the same.

i mean, as example, it is not working right for 2 circles that the small one is inside the big one.

(MartĂ­ Angelats i Ribera) #10

What algorithm are you using?

you should be using something like this:

public static function circlesColide(center1:Point, r1:Number, center2:Point, r2:Number):Boolean
{
    var x:Number = center2.x - center1.x;
    var y:Number = center2.y - center1.y;
    
    return (x*x + y*y) <= (r1*r1 + r2*r2);
}

Edit: Unecessary Math.abs. I don’t know why i used it.

(Bora Kasap) #11

hey man, i don’t understand what are you trying because it is not working for my situation, or i don’t know how to implement your way… i am using this [SOLVED] Modifying nearestToEntity() to nearestCircleToCircle

var nearestUnit:Unit = Unit(this.world.nearestCircle("unit", spellinstance));
				if (nearestUnit != spellinstance.caster && spellinstance.distanceFrom(nearestUnit) < spellinstance.radius + nearestUnit.radius) {
					if ((this.enemy && nearestUnit.isEnemyOf(spellinstance.caster)) || (this.ally && !nearestUnit.isEnemyOf(spellinstance.caster))) {
						this.world.remove(this);
						this.world.remove(spellinstance);
						if (unitaction != "") UnitActions.apply(this.unitaction, nearestUnit);
					}
				}
(MartĂ­ Angelats i Ribera) #12

The function above checks if two circles collide or not. The parameters works this way:

if (circlesCollide(centerCircle1, radiusCircle1, centerCircle2, radiusCircle2))
{
    //do something
}

I don’t know how are you using it but the problem might be there.

I’m not sure what everything does but here is my blind gess:

var unit:Unit = this.world.nearestCircle("unit", spell) as Unit;
if (unit !== spell.caster
&& circlesCollide(unit.position, unit.radius, spell.position, spell.radius)
&& ((this.enemy && unit.isEnemyOf(spell.caster)) || (this.ally && !unit.isEnemyOf(spell.caster))
{
    //do stuff
}

PS: I shorted the names so it was more readable.

PS2: You can modify the function to use x and y isntead of the points, which is probably easier if you are using Entities

(Bora Kasap) #13

your function doesn’t work right man, i am sorry, i don’t know why, i’m trying to do your way since last 2 hours but it is just making me crazy…

so, i back to use this and everything works fine again

public function collideCircle(x2:Number, y2:Number, size2:Number):Boolean
		{
			return Math.sqrt((x2 - this.x) * (x2 - this.x)  + (y2 - this.y) * (y2 - this.y)) < (size2 + this.size);
		}
(Kyle) #14

This should really really really really work.

public function collideCircle(x2:Number, y2:Number, size2:Number):Boolean
{
    // No Math.sqrt, so the distance is the square of the actual distance
    // And the distance threshold of the circles was also squared
    return (x2 - this.x) * (x2 - this.x)  + (y2 - this.y) * (y2 - this.y) < (size2 + this.size) * (size2 + this.size);
}

Again, it’s your choice if you would want to implement this. We just want to share how you can improve the function in terms of performance.

(Bora Kasap) #15

it worked, but really i have no idea what is happening here :smiley: thanks

(MartĂ­ Angelats i Ribera) #16

It’s the exact same algorith as mine but in a single line and using x and y instead of a point.

By the way, you may want to use smaller or equal (<=) istead of smaller (<), if you want to detect if they touch (if they are tengent to each other).

(Zachary Lewis) #17

Math explaining time!

This all works around the Pythagorean theorem. The sum of the square of the lengths of the two shorter sides of a right triangle equals the square of the length of the third side. Written out, it’s a mouthful. Here’s a picture.

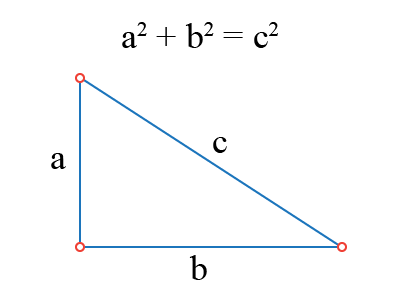
Now, to actually find the distance of c, you’d need to take the square root of c; however, for the problem of two circles, determining the actual distance from the centers of the circles isn’t needed to determine if they touch.

Let’s take our two circles and place them on the two points that make up side c.

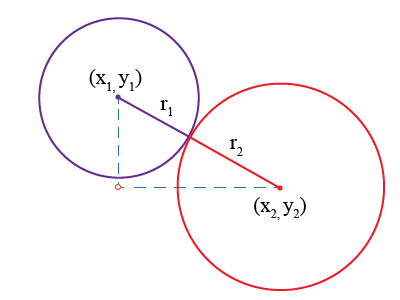
We know the center of the circles, (x1, y1) and (x2, y2), as well as each circle’s radius, r1 and r2. From here you can see that the sum of the radii, r1 + r2, is identical to c. We also know the relationship between sides a and b with respect to c.

Since we know the center points of our two circles, we can calculate a and b in terms of our two circles and plug it back into Pythagoras’s theorem.

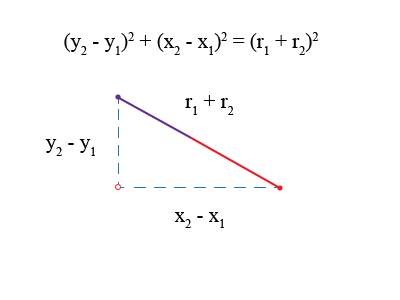
We can use this new equation to determine if the two circles are colliding or not without having to take the square root at all. The function would look identical to the solution @Copying provided above.

function circlesColide(center1:Point, r1:Number, center2:Point, r2:Number):Boolean
{
    var x:Number = center2.x - center1.x;
    var y:Number = center2.y - center1.y;
    
    return (x*x + y*y) <= (r1*r1 + r2*r2);
}

A solution using square roots wouldn’t be an incorrect solution to this problem; however, the reason this function is preferable is due to the way computers work. A computer is designed to add numbers really, really quick. Multiplication is just repeated addition, so they can multiply really quick as well.

Finding the square root of a number is a really complex and tricky algorithm that takes much longer than it would take to just add a bunch of stuff together; therefore, avoiding it will increase the execution speed of your program.

I hope this helps you understand all of this a bit better!

(MartĂ­ Angelats i Ribera) #18

I didn’t expect you to make this detailed explained post. It’s well explained and the images are pretty nice. I like it :stuck_out_tongue: