Note for those encountering this by search:
NotARaptor solves this solution elegantly and brilliantly, but I was too foolish to understand his solution. I ultimately fixed my own solution, although the result looks imperfect (I just happened to like the imperfect look). I will present both solutions here.
The PROBLEM
okay, so the look im going for is fairly simple, but the implementation is tricky. The idea is to create a spiraling pattern that moves from the subject to the target at any angle, heres my worst possible rendition of what this might look like drawn in MS paint:
My SOLUTION
Let me go through my though process so far.
so, we start with a
var direction:Point which holds coordinates on a unit circle between 0 and 1 – we found these by using our friends sine and cosine of the angle to the mouse coordinates from the subject.
Essentially, this point holds the direction we want to fire the spiral bullet by finding what percentage of your speed you ought to move in the X direction, and what percent in the Y direction:
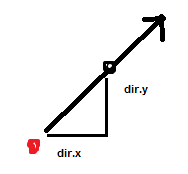
So far, so good. Next I want to find the angle of the line perpendicular to this function. we find this by taking the angle of the first direction
var angle:Number = Math.atan2(dir.x, dir.y)
and subtracting it from 90 degrees to get the complementary angle.
var pAngle:Number = -rightAngle + angle
Again, we’re working with the unit circle, so our values are between 0 and 1. This helps us with our math, because we KNOW that the HYPOTENUSE on a unit circle is ALWAYS equal to 1.
we find our perpendicular direction x and y using sine and cosine again:
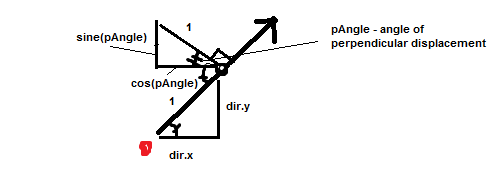
okay, so far so good, so now we have two unit circle coordinates, representing the movement components ALONG the target vector and PERPENDICULAR TO the target vector
var dir:Point;
var dirPerpendicular:Point;
The final code works like this:
// determine angle of movement
var angle:Number = Math.atan2(dir.x, dir.y)
// determine complement
var complAngle:Number = ( -rightAngle + angle)
// determine perpendicular compnents
var perpX:Number = Math.cos(complAngle)
var perpY:Number = Math.sin(complAngle)
// determine displacement. Multiply the unit circle values by the speed to get the x and y
// components of movement
var normalDisplacement:Point = new Point(dir.x * speed, dir.y * speed)
var perpendicularDisplacement:Point = new Point(perpX *speed/2, perpY * speed/2)
if (!rising)
{
perpendicularDisplacement.x *= -1
perpendicularDisplacement.y *= -1
}
// determine the new final positions by summing the displacements
var newX:Number = normalDisplacement.x + perpendicularDisplacement.x;
var newY:Number = normalDisplacement.y + perpendicularDisplacement.y;
// tween the values to their new locations. Of the two values,
// dir.x and dir.y, the larger value should be tweened linearly, and
// the smaller value should use Ease.sineInOut
aTween.tween(subject, "x", subject.x + newX, time, Math.abs(dir.x)>Math.abs(dir.y)? null : Ease.sineInOut)
bTween.tween(subject, "y", subject.y + newY, time, Math.abs(dir.x)>Math.abs(dir.y)? Ease.sineInOut: null)
it still looks a little unlike my original vision on the diagonals, but it creates the effect i’m going for, and in Actually, I think the look of the diagonal spiral is pretty cool! lets face it, I’m not using this for drone strike targeting, I’m just making a video game. Pretty cool looking is the best I need to create.
press the “e” key to fire
(for reference this is the earlier, screwed up version, the working code is down at the bottom) FromScratch.swf(65.6 KB)
NotARaptor’s SOLUTION
see below

